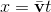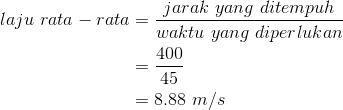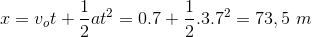Kinematika Gerak Lurus Beraturan (GLB) & Gerak Lurus Berubah Beraturan (GLBB)
Pengenalan Kinematika
Kinematika, adalah suatu cabang dalam ilmu mekanika yang khusus mempelajari tentang gerak objek / partikel berdasarkan pengukuran geometri tanpa melihat gaya penyebab gerakan tersebut. Karakteristik gerak suatu benda ditinjau dari posisi, kecepatan dan percepatan.
Jadi, Kinematika bisa disimpulkan adalah :
- Menjelaskan tentang gerak berdasarkan dari pengukuran geometri dari suatu benda/partikel
- Menggunakan ilmu matematika untuk menjelaskan definisi “gerak”, ditinjau dari “posisi”, “kecepatan” dan “percepatan”
Berikut adalah pembahasan kinematika pada situs ini :
- Kinematika : Gerak Lurus Beraturan dan Gerak Lurus Berubah Beraturan
- Kinematika : Gerak Jatuh Bebas, Parabola dan Gerak Lurus dengan Percepatan Variabel
- Kinematika : Gerak Rotasi
Mari kita simak pembahasan kinematika gerak lurus benda ditinjau dari komponen - komponennya secara satu persatu.
Jarak dan Perpindahan
Untuk memahami perbedaan jarak dan perpindahan, bisa ditinjau dari definisi kedua kata tersebut.
Jarak adalah panjang seluruh lintasan yang ditempuh.
Jarak adalah panjang seluruh lintasan yang ditempuh.
Perpindahan adalah jarak dan arah dari posisi awal ke posisi akhir.
Untuk lebih memperjelas lagi, mari kita simak gambar berikut ini :
 |
| Gambar K1 - Ilustrasi posisi antara 2 titik A dan C (Fisika SMU) |
Penjelasan pada gambar K1 tersebut :
- Gambar (a) : Jarak dari AC = 7 langkah
- Gambar (b) : Perpindahan dari AC = 1 langkah, dengan perpindahannya adalah sebagai berikut :
- Perpindahan AB = 4 langkah ke Timur
- Perpindahan BC = 3 langkah ke Barat
- Perpindahan AC = AB + BC = 4 + (-3) = 1 langkah ke Timur
Mari kita simak lagi pada gambar K2 berikut:
 |
| Gambar K2 - Ilustrasi perpindahan dari posisi P ke Q (Fisika SMU) |
Pada gambar K2, perpindahan suatu partikel ketika
bergerak di sepanjang lintasannya dari titik pertama (titik P) ke titik kedua (titik Q) didefinisikan sebagai vektor ∆x yang ditarik dari titik pertama ke
titik kedua.
Jadi, pada gambar K2 vektor PQ, yang besarnya :
- x2 – x1 = ∆x
- ∆x adalah perpindahan partikel tersebut.
Kinematika Gerak Lurus Beraturan (GLB) & Gerak Lurus Berubah Beraturan (GLBB)
Gerak Lurus Beraturan - GLB
Benda / partikel yang bergerak dengan kecepatan tetap dikatakan melakukan gerakan lurus beraturan (GLB).Hal ini dapat dipenuhi apabila :
- arah gerak benda tetap (lintasan lurus)
- kelajuan benda tidak berubah
Gerak Lurus Berubah Beraturan - GLBB
Suatu benda / partikel dikatakan mengalami gerak lurus berubah beraturan, jika benda / partikel tersebut memiliki percepatan yang tetap (konstan). Artinya pada setiap selang waktu yang sama, kecepatan benda bertambah dengan besar yang sama.
Untuk lebih memahami mengenai GLB dan GLBB ini, mari kita bahas satu - persatu komponen dari tipe gerak tersebut.
Kelajuan & Kecepatan
Kelajuan atau kecepatan didefinisikan sebagai perubahan jarak tiap satuan waktu. Perbedaan antara kelajuan dan kecepatan, ditinjau dari arahnya. Kelajuan adalah besaran skalar, dan kecepatan adalah besaran vektor, dimana arah dari gerak tersebut diperhitungkan.
Perhatikan gambar K3 berikut mengenai kecepatan rata - rata dan kecepatan sesaat.
Perhatikan gambar K3 berikut mengenai kecepatan rata - rata dan kecepatan sesaat.
 |
| Gambar K3 - Grafik perubahan posisi dari titik p ke q pada selang waktu (Fisika/Sears Zemansky) |
Kecepatan Rata - Rata
Kecepatan rata – rata adalah
perbandingan perpindahan suatu benda / partikel dari titik awal dalam x2
– x1 = ∆x dalam selang waktu t2 – t1 = ∆t,
sehingga bisa dituliskan sebagai berikut :
Persamaan 1) ini bisa ditulis menjadi :
Berdasarkan persamaan 2) tersebut, jika :
- t1 = 0
- t2 adalah waktu sembarang t ( t2 = t )
- x1 adalah koordinat ketika t = 0, disebut titik awal xo ( x1 = xo )
- x2 adalah koordinat pada waktu t ( x2 = x )
maka persamaan tersebut bisa
ditulis :
Jika pada t1 = 0, xo = 0
maka persamaan tersebut menjadi :
Kecepatan Sesaat
- Kecepatan sesaat didefinisikan sebagai kecepatan suatu partikel pada suatu saat atau pada satu titik di lintasannya.
- Pada gambar K3 tersebut, kecepatan sesaat pada titik p besarnya dihitung dengan limit ∆t menuju 0 atau ditulis (lim ∆t → 0)
- Jika v adalah symbol untuk kecepatan sesaat, maka besarnya adalah
Percepatan & Perlajuan
Sebuah batu yang menggelinding dari atas bukit memiliki kecepatan yang semakin lama semakin bertambah selama pergerakannya. Batu yang menggelinding tersebut dikatakan dipercepat. Dalam kajian kinematika gerak lurus, perubahan kecepatan tiap satuan waktu dinamakan percepatan.
Karena kecepatan merupakan besaran vektor, maka percepatan juga merupakan besaran vektor. Sedangkan perlajuan, merupakan besaran skalar dari percepatan.
Ilustrasi percepatan bisa dilihat pada gambar K4 berikut :
 |
| Gambar K4 - Ilustrasi perubahan kecepatan suatu benda dari titik P dan Q (Fisika/Sears Zemansky) |
Pada gambar tersebut, sebuah benda bergerak dengan kecepatan v1 pada titik P, kemudian mengalami perubahan kecepatan pada titik Q menjadi v2.
Mari simak gambar grafik K5 mengenai perubahan kecepatan berikut dalam penjelasan mengenai percepataan rata - rata dan percepatan sesaat.
 |
| Gambar K5 - Grafik perubahan kecepatan dari posisi p ke posisi q (Fisika/Sears Zemansky) |
Percepatan Rata - rata
- Percepatan rata – rata benda / partikel selama bergerak dari p ke q didefinisikan sebagai perbandingan antara perubahan kecepatan terhadapa selang waktu.
- Rumusan percepatan rata – rata ditulis sebagai berikut :
Jika :
- t1 = 0
- t2 adalah waktu sembarang t ( t2 = t )
- v1 adalah koordinat ketika t = 0, disebut titik awal vo ( v1 = vo )
- v2 adalah koordinat pada waktu t, ( v2 = v )
maka persamaan 6) tersebut bisa
ditulis menjadi :
Kecepatan Rata - rata pada Percepatan Konstan
Perhatikan ilustrasi grafik K6 berikut :
 |
| Gambar K6 - Ilustrasi grafik kecepatan - waktu untuk gerak lurus dengan percepatan konstan (Fisika/Sears Zemansky) |
Untuk menentukan perpindahan
sebuah benda/partikel yang bergerak dengan percepatan konstan, kecepatan rata –
rata dalam sembarang waktu t, adalah setengah dari penjumlahan kecepatan pada
awal dan pada akhir selang waktu, sehingga bisa dituliskan :
Percepatan Sesaat
- Didefinisikan sebagai percepatan pada saat tertentu atau pada suatu tutuk tertentu di lintasannya.
- Pada gambar tersebut, percepatan sesaat besarnya dihitung dengan limit ∆t menuju 0 atau ditulis (lim ∆t → 0)
- Jika a adalah simbol untuk percepatan sesaat, maka besarnya adalah
Perpindahan Benda / Partikel pada Percepatan Tetap
Perhatikan grafik gambar K7 berikut :
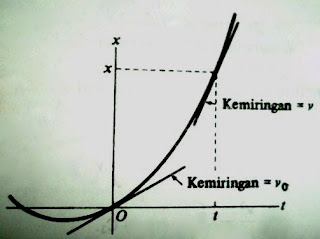 |
| Gambar K7 - Ilustrasi grafik koordinat - waktu untuk gerak dengan percepatan konstan |
Telah diketahui, bahwa perpindahan adalah kecepatan rata - rata yang ditempuh dalam waktu tertentu, berdasarkan dari persamaan 4) :
Untuk menentukan seberapa jauh perpindahan benda / partikel pada percepatan tetap, perumusannya bisa dengan menggabungkan persamaan 8) dan 7) ke persamaan 4), dijabarkan sebagai berikut :
Jika nilai t dari persamaan 7) dan persamaan 8) dimasukkan ke persamaan 4), menjadi
Persamaan - persamaan 7), 9) dan 10) adalah persamaan gerak dengan percepatan konstan. khusus untuk keadaan di mana benda / partikel berada di titik pangkal pada saat t = 0.
Persamaan 9) ditunjukkan dalam grafik K7 berupa garis lengkung kurva tersebut. Garis lengkung itu berupa parabola. Kemiringan garis singgung pada t = 0 sama dengan kecepatan awal vo dan kemiringan garis singgung pada saat t sama dengan kecepatan v pada saat t tersebut.
Untuk lebih memahami penggunaan rumus - rumus di atas, simak contoh soal berikut.
Contoh Soal Beserta Pembahasannya
Soal 1 :
Seorang pelari menempuh satu putaran sepanjang 400 m dalam waktu 45 detik. Tentukan :
- Berapa kelajuan rata - ratanya?
- Berapakah kecepatan rata - ratanya?
Jawab
→ Kelajuan rata - rata :
→ Kecepatan rata - ratanya :
karena titik akhir lintasan berhimpit dengan titik awalnya, maka vektor perpindahan pelari itu adalah 0, sehingga kecepatan rata - ratanya = 0 m/s.
→ PS : Jika masih ada yang bingung mengapa kecepatan rata - ratanya = 0 m/s. Perhatikan bahwa kecepatan adalah besaran vektor, sehingga titik awal dan titik akhir menentukan hasil perhitungan. Titik awal sama dengan titik akhir, sehingga benda dianggap tidak bergerak berdasarkan arah vektornya.
Soal 2 :
Benda yang mula - mula diam dipercepat dengan percepatan 3 m/s² dan menempuh garis lurus. Tentukan :
- laju pada akhir detik ke-7 ?
- laju rata - rata dalam selang waktu 7 detik pertama ?
- jarak yang ditempuh dalam 7 detik tersebut ?
Jawab
→ Laju pada akhir detik ke-7 :
Gunakan persamaan 7) di atas :
→ Laju rata - rata dalam selang waktu 7 detik pertama :
Gunakan persamaan 8) di atas :
→ Jarak yang ditempuh dalam 7 detik tersebut :
Gunakan persamaan 9) sebelumnya :
Soal 3 :
Laju sebuah truk bertambah secara teratur dari 20 km/jam, menjadi 80 km/jam dalam waktu 26 detik. Carilah :
- laju rata - rata truk tersebut ?
- percepatan truk tersebut ?
- jarak yang ditempuh oleh truk tersebut ?
Jawab
Diketahui :
Soal 4 :
Bola jatuh bebas dari ketinggian 30 m. Tentukan :
- Berapakah laju bola sesaat sebelum sampai di tanah?
- Berapa waktu yang diperlukan bola untuk mencapai tanah?
Jawab
Soal 5 :
Mobil dengan laju 33 m/s mengalami perlambatan hingga dalam waktu 7 detik lajunya tinggal 12 m/s. Tentukan :
- Percepatan mobil tersebut ?
- Jarak yang ditempuh mobil dalam detik keempat ?
Jawab
Review Rumus Kinematika Gerak Lurus
Untuk lebih mengasah kemampuan belajar teman - teman, silakan mencoba mengerjakan soal - soal di bawah ini
Problem / Soal
Soal 1 : Sebuah mobil yang mula - mula diam bergerak dengan percepatan tetap sehingga 10 detik sesudah bergerak, kecepatannya menjadi 80 km/jam. Tentukan
- berapa kecepatan rata - rata mobil ?
- berapa percepatan mobil ?
- berapa selang waktu yang dibutuhkan untuk mencapai kecepatan 60 km/jam?
- berapa perpindahan mobil selama 10 detik pertama?
Soal 3 : Seorang pengendara motor mengendarai kendaraannya ke Utara dengan kecepatan 85 km/jam selama 35 menit. Kemudian ia berhenti selama 15 menit, sebelum meneruskan perjalanannya dalam arah yang sama sejauh 130 km dalam waktu 2 jam. Tentukan :
Soal 4 : Seorang atlit renang jarak 100 m dapat menyelesaikan lintasan 50 m pertama dalam waktu 20 detik dan lintasan 50 kedua dalam waktu 22 detik. Tentukan :
Soal 5 : Sebuah benda bergerak dengan kecepatan awal vo = 60 m/s. Kemudian benda tersebut berhenti sesudah bergerak sejauh 15 km karena diperlambat. Berapakah percepatan rata - rata benda selama 15 detik?
- Berapakah keseluruhan perpindahan pengendara sepeda motor tersebut?
- Berapakah kecepatan rata - rata sepeda motor?
- Kecepatan rata - rata perenang untuk 50 m pertama?
- Kecepatan rata - rata perenang untuk 50 m kedua?
- Kecepatan rata - rata perenang dalam menempuh jarak 100 m?
Soal 6 : Sebuah mobil bergerak dalam lintasan lurus, dengan kecepatan sesaat 30 m/s. Dua detik kemudian, kecepatannya menjadi 25 m/s. Berapakah percepatan rata - rata kendaraan selama selang waktu tersebut ?
Soal 7 : Sebuah mobil balap dipacu sehingga kecepatannya bertambah dari 44 m/s menjadi 66 m/s pada suatu jalanan yang lurus. Berapakah percepatan mobil itu?
Soal 8 : Seorang anak sedang mengendarai sepeda. Pada saat t = 0, kecepatannya 8 m/s dan pada saat t = 20 detik, kecepatannya menjadi 20 m/s. Berapakah percepatan rata - rata anak itu selama selang waktu di atas?
Soal 9 : Sebuah pesawat terbang mendarat dengan keceaptan 100 m/s, kemudian diperlambat dengan 5 m/s² sampai berhenti. Tentukan :
Soal 10 : Sebuah benda bergerak vertikal ke atas dari permukaan bumi dengan kecepatan awal vo m/s, percepatan gravitasi g dan tinggi maksimum yang dicapai h. Jika benda tersebut dilempar pada sebuah planet dengan kecepatan awal 2vo dan percepatan gravitasi 2g, berapakah ketinggian maksimum yang dapat dicapai benda ?
- Sesaat setelah menyentuh landasan, berapakah waktu yang diperlukan untuk menghentikan pesawat itu?
- Apakah pesawat tersebut dapat mendarat pada lapangan terbang yang panjang landasannya 0,8 km?
Soal 11 : Sebuah bola dilempar tegak lurus ke bawah dari ketinggian 300 m dengan kecepatan awal 8 m/s. Berapakah waktu yang diperlukan bola untuk mencapai tanah?
Soal 12 : Sebuah batu dilepaskan dari atas sebuah gedung pada ketinggian tertentu. Setelah 2 detik, batu kedua dilemparkan ke bawah dengan kecepatan awal 30 m/s. Jika kedua batu tiba di tanah dalam waktu bersamaan, maka dari ketinggian berapakah kedua batu dilepaskan?
Soal 13 : Seorang siswa menerjunkan diri dari papan kolam renang setinggi 8 meter tanpa kecepatan awal. Jika massa siswa 40 kg dan percepatan gravitasi 9,8 m/s² maka berapa kecepatan siswa tersebut saat tercebur ke air?
Soal 14 : Sebuah benda yang jatuh bebas membutuhkan waktu 1,5 detik untuk menjalani ketinggian 30 meter terakhir sebelum tiba di tanah. Dari ketinggian berapakah benda tersebut dilepaskan, jika percepatan gravitasi = 9,7 m/s² ?
Soal 15 : Sebuah bola dilemparkan vertikal ke atas dengan kecepatan 35 m/s. Dengan mengabaikan gesekan udara, tentukan :
- hitunglah ketinggian maksimum yang dapat dicapai?
- waktu yang diperlukan untuk mencapai ketinggian tersebut?
- kecepatan sesaat pada akhir detik ke 30 ?
- kapan bola itu mencapai ketinggian 100 m?
-- Kinematika Gerak Lurus Beraturan dan Gerak Lurus Berubah Beraturan
Pembahasan soal beserta jawaban akan segera menyusul. Jika ada kesalahan pengetikan atau perhitungan, mohon untuk dikoreksi agar tidak terjadi kekeliruan bagi teman - teman yang belum mengerti.
Mudah - mudahan tulisan ini bisa bermanfaat untuk yang membutuhkan. Saran dan masukan yang membangun bisa melalui komentar.
Salam 😊
Credits :
Photo by Kamshotthat by pexels.com
Incoming Search Terms
- kinematika gerak
- GLBB
- gerak lurus berubah beraturan
- GLB
- gerak lurus